Harmonic Spectrum (諧波譜)
除了 envelope 會影響音色外,我們還要分析聲音在不同頻率下的振幅。我們稱作 聲音的 harmonic spectrum。高高低低的 envelope 代表隨著時間而改變的振幅。
harmonic spectrum represents the amplitude of each frequency at a given point in time.
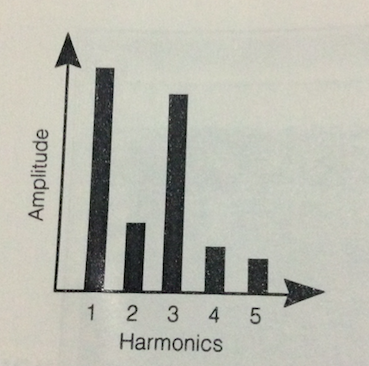
要了解 harmonic spectrum 的原理,需要了解三個科學理論:
- Sauveur
- Fourier
- Helmholtz
Overtones
1970 年代 Joseph Sauveur 發現了 overtone series(泛音列),發現聲音頻率之間有倍數之間的關係。泛音列中最低的音「基音」(fundamental)是第一泛音,在這個 case 裡是 110 Hz,音符 A。所有有週期性的震動都有泛音,有比例之間的關係。如果一個聲音沒有泛音他可能是基音或是 sine wave 波型的聲音。Sine wave 的聲音例如人吹口哨的聲音,或是用 electronic oscillator 所產生的聲音,都是屬於 sine wave 的波型。
如果你知道第一泛音的頻率,又知道泛音之間的比例,你就可以算出其他泛音的值。吹奏銅管樂器(像 trumpet 或 bugle),可以透過改變嘴唇震動的頻率去吹出不同音高的泛音。
Overtone series: the phenomenon that complex sounds contain frequencies following a common pattern of ratios.

其次的最低的音是第二泛音,依此類推。基音上方的其他音叫做「上方泛音」(upper partials 或 overtones),他們與基音之間的音程是固定的:一個八度,然後是一個純五度,等等。通常,樂器上發出的每個音都是基音和上方泛音的複合音。
Overtones 又稱作 harmonic ,first harmonic 就是基音( fundamental),另外還有 partial 這個詞,partial 的同義詞就是 harmonic。
- first harmonic 等於 fundamental
- first overtone 等於 second harmonic or second partial
- second overtone 等於 third harmonic and partial 細節可參考 Wiki
Harmonic Spectrum and Fourier's Theorem
Fourier's Theorem 說任何有週期性的 vibration 都可以用 a series of sine waves 來呈現。
- We can add sine waves to make increasingly complex sounds(additive synthesis
- We can take a complex sound and subtract sine waves to make simpler sounds(subtractive synthesis)
- We can analyze any sound by identifying the amplitude of every sine wave in overtone series present in sound(spectrum or harmonic analytisis)
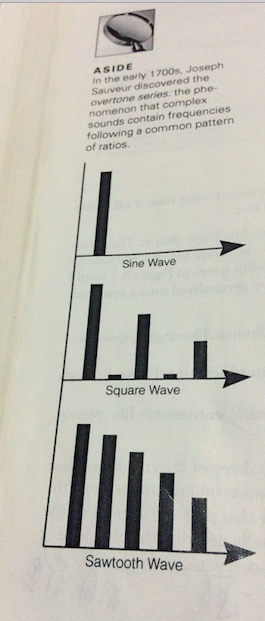
你會發現 sine wave 沒有泛音列(overtones),square wave 的泛音則是長得怪怪的。
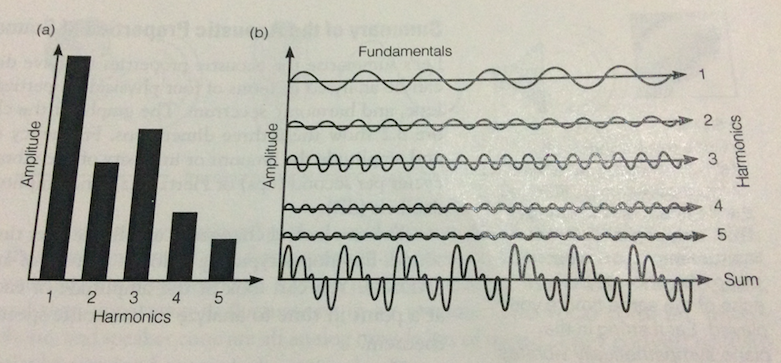
下面這二張圖就是個好例子,左邊的圖是五個泛音的振幅,右圖就是五個泛音的 sine wave 加上最後的加總(the "sum" of sine waves),左圖可以用 spectrum analyzer 分析出來,右圖則是用 oscilloscope(示波器) 去分析。
- Electronic oscillators used in analog synthesizers are commonly sine, square, and sawtooth oscillators.
不同的 harmonic spectrum 會造就不同的音色,每種樂器都有他獨特的 harmonic spectrum。書中舉了單簧管、雙簧管跟長笛作為例子。
- Changes in harmonic spectrum of a sound are perceived as changes in timbre. Clarinet sounds favor the odd harmonics like the electronic square wave. Rich sounds like oboes have lots of harmonics at strong amplitudes. Flute sounds favor the octave harmonics.
了解泛音的組成(harmonic makeup)對於數位合成器(digital sound synthesis)的使用相當重要。